Skip to main content

Sieve of Eratosthenes

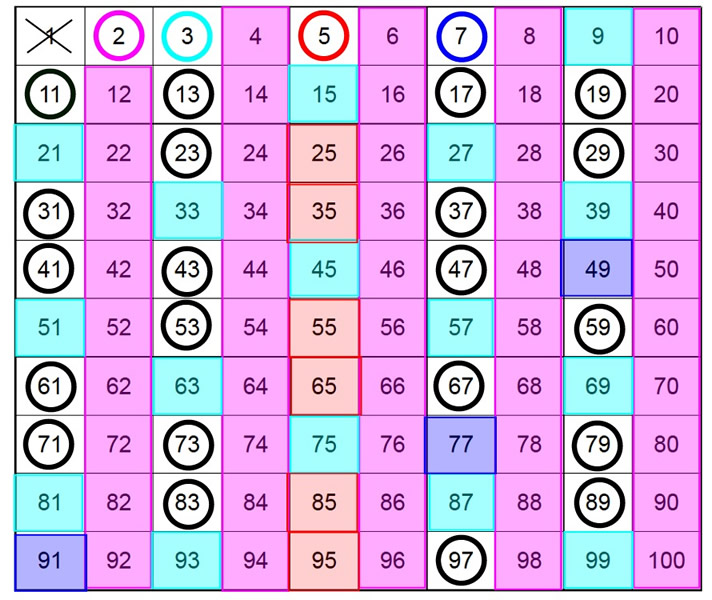
The Sieve of Eratosthenes is an ancient algorithm used to find all prime numbers up to a given limit. It works by iteratively marking the multiples of each prime number starting from 2.

Algorithm Steps:​

  1. Create a list of consecutive integers from 2 to n.
  2. Start with the first number, mark it as prime, and then mark all of its multiples as composite (not prime).
  3. Move to the next unmarked number and repeat the process.
  4. Continue until all multiples of primes have been marked.
Sieve of Eratosthenes

JavaScript Implementation​

function sieveOfEratosthenes(n) {
  const primes = new Array(n + 1).fill(true);
  primes[0] = primes[1] = false;

  for (let i = 2; i <= Math.sqrt(n); i++) {
    if (primes[i]) {
      for (let j = i * i; j <= n; j += i) {
        primes[j] = false;
      }
    }
  }

  return primes.map((isPrime, index) => isPrime ? index : null).filter(Boolean);
}

console.log(sieveOfEratosthenes(30)); // Output: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29]

This implementation has a time complexity of O(n log log n).