Stack Pattern
Introduction
Stacks are a fundamental data structure that follows the Last In, First Out (LIFO) principle. This means that the most recently added element is the first one to be removed. Stacks are used in various algorithms and problems, such as parsing expressions, managing function calls, and backtracking.
Key Operations
- Push: Add an element to the top of the stack.
- Pop: Remove the element from the top of the stack.
- Peek: View the top element of the stack without removing it.
- isEmpty: Check if the stack is empty.
Stack Implementation Using a LinkedList
// Node class represents each element in the stack
class Node {
constructor(value, next = null) {
this.value = value; // The value stored in the node
this.next = next; // Reference to the next node in the stack
}
}
// Stack class manages the stack operations using a linked list
class Stack {
constructor() {
this.top = null; // Points to the top node in the stack
this.size = 0; // Tracks the number of elements in the stack
}
// Adds a new value to the top of the stack
push(value) {
this.top = new Node(value, this.top); // Create a new node pointing to the current top
this.size++; // Increment the size of the stack
}
// Removes and returns the value from the top of the stack
pop() {
if (!this.top) return null; // If the stack is empty, return null
const value = this.top.value; // Get the value of the top node
this.top = this.top.next; // Move the top pointer to the next node
this.size--; // Decrement the size of the stack
return value; // Return the value of the popped node
}
// Returns the value at the top of the stack without removing it
peek() {
return this.top ? this.top.value : null; // Return top value or null if stack is empty
}
// Checks if the stack is empty
isEmpty() {
return !this.top; // Returns true if top is null
}
// Returns the current size of the stack
getSize() {
return this.size; // Return the number of elements in the stack
}
}
// Example usage:
const stack = new Stack();
stack.push(10); // Add 10 to the stack
stack.push(20); // Add 20 to the stack
stack.push(30); // Add 30 to the stack
console.log(stack.peek()); // 30 (top value)
console.log(stack.pop()); // 30 (removes and returns the top value)
console.log(stack.getSize()); // 2 (size of the stack after pop)
console.log(stack.isEmpty()); // false (stack is not empty)
Stack Implementation ( Array Based)
1. Array-based: Uses a simple array with a size tracker for O(1) operations
2. Memory Efficient:
- Trims array on pop to free memory
- Only stores actual elements, no empty spaces
3. Operations:
- push: O(1)
- pop: O(1)
- peek: O(1)
- isEmpty: O(1)
- getSize: O(1)
class Stack {
constructor() {
this.items = [];
this.size = 0;
}
// Push element onto stack
push(element) {
this.items[this.size] = element;
this.size++;
return this.size;
}
// Remove and return top element
pop() {
if (this.isEmpty()) {
throw new Error("Stack Underflow");
}
this.size--;
const item = this.items[this.size];
this.items.length = this.size; // Trim array to free memory
return item;
}
// Return top element without removing
peek() {
if (this.isEmpty()) {
throw new Error("Stack is empty");
}
return this.items[this.size - 1];
}
// Check if stack is empty
isEmpty() {
return this.size === 0;
}
// Get current size
getSize() {
return this.size;
}
// Clear stack
clear() {
this.items = [];
this.size = 0;
}
// Convert stack to array
toArray() {
return [...this.items];
}
}
const stack = new Stack();
stack.push(1);
stack.push(2);
console.log(stack.pop()); // 2
console.log(stack.peek()); // 1
Common Patterns
1. Balanced Parentheses
Stacks are often used to validate balanced parentheses in expressions. The basic idea is to push each opening parenthesis onto the stack and pop from the stack when a closing parenthesis is encountered. If the stack is empty at the end, the parentheses are balanced.
Example Problem: Valid Parentheses
function isValid(s) {
const stack = [];
const map = { ')': '(', '}': '{', ']': '[' };
for (let char of s) {
if (map[char]) {
if (stack.pop() !== map[char]) return false;
} else {
stack.push(char);
}
}
return stack.length === 0;
}
Monotonic Stack
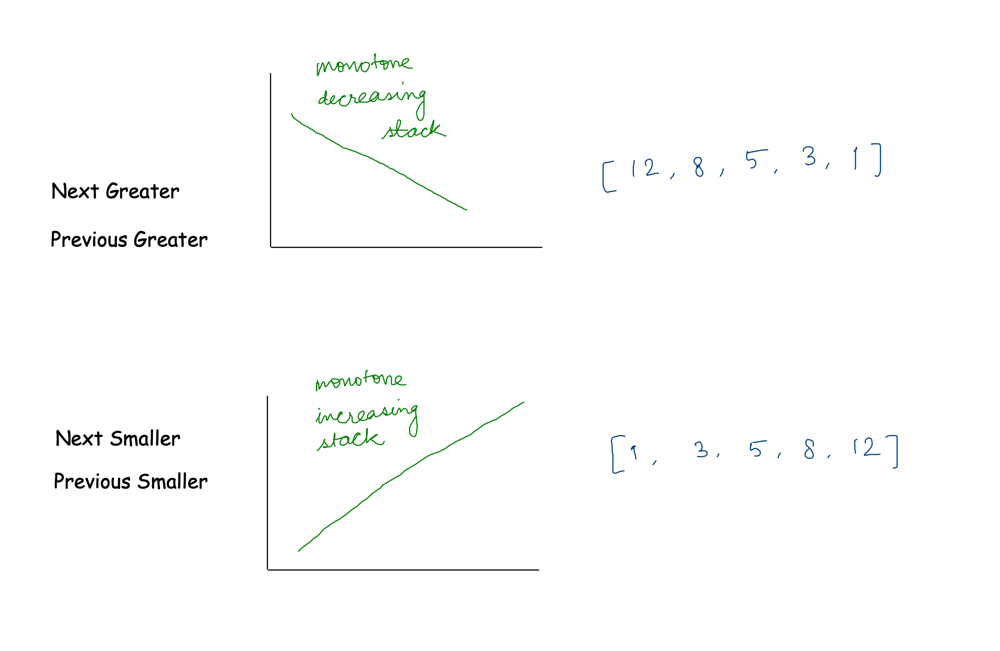
Image Source By: (https://leetcode.com/u/darkalarm/)
Introduction
A monotonic stack is a stack that maintains a specific order of its elements. It can be either monotonic increasing or monotonic decreasing, depending on the problem requirements. This type of stack is useful for solving problems involving ordered data efficiently.
Key Concepts
- Monotonic Increasing Stack: Maintains elements in increasing order from top to bottom. Useful for finding the next smaller element.
- Monotonic Decreasing Stack: Maintains elements in decreasing order from top to bottom. Useful for finding the next greater element.
Monotonic Stack Variations
Monotonic stacks are used to solve problems involving ordered data by maintaining a specific order of elements. The table below summarizes various monotonic stack types and their typical use cases.
Table of Variations
| Stack Type | Order Maintained | Use Case | Example Problem |
|---|---|---|---|
| Monotonic Increasing Stack | Elements in increasing order | Finding the next smaller element | Next Smaller Element I |
| Monotonic Decreasing Stack | Elements in decreasing order | Finding the next greater element | Next Greater Element I |
| Monotonic Increasing Stack | Elements in increasing order | Finding the maximum rectangle in histogram | Largest Rectangle in Histogram |
| Monotonic Decreasing Stack | Elements in decreasing order | Finding the next greater element in a circular array | Next Greater Element II |
| Monotonic Decreasing Stack | Elements in decreasing order | Finding the minimum number of operations needed to reduce to zero | Trapping Rain Water |
| Monotonic Increasing Stack | Elements in increasing order | Checking for valid parentheses or balanced expressions | Valid Parentheses |
| Monotonic Decreasing Stack | Elements in decreasing order | Finding the next smaller element in a circular array | Next Smaller Element II |
Explanation
-
Monotonic Increasing Stack: This stack maintains elements in increasing order from top to bottom. It's useful for problems where you need to find the next smaller element or the maximum rectangle in a histogram.
-
Monotonic Decreasing Stack: This stack maintains elements in decreasing order from top to bottom. It's helpful for problems where you need to find the next greater element or solve problems related to trapped water.
Applications
1. Next Greater Element
Problem: Given an array of integers, find the next greater element for each element. If no such element exists, output -1.
Solution: Use a monotonic decreasing stack to track elements in decreasing order. Iterate through the array from left to right. For each element, pop from the stack until the top of the stack is greater than the current element. The top of the stack is the next greater element for the current element.
Example Problem: Next Greater Element I
function nextGreaterElements(nums) {
const stack = [];
const result = Array(nums.length).fill(-1);
for (let i = 0; i < nums.length * 2; i++) {
const num = nums[i % nums.length];
while (stack.length && nums[stack[stack.length - 1]] < num) {
result[stack.pop()] = num;
}
if (i < nums.length) stack.push(i);
}
return result;
}
Monotonic Stack Pattern Template
const CASES = Object.freeze({
'NEXT_GREATER': 'NEXT_GREATER',
'PREV_GREATER': 'PREV_GREATER',
'NEXT_SMALLER': 'NEXT_SMALLER',
'PREV_SMALLER': 'PREV_SMALLER'
})
function monotonicStackTemplate(arr, type) {
let result = new Array(arr.length).fill(-1);
let stack = [];
for (let i = 0; i < arr.length; i++) {
let condition;
let assignmentPos;
switch (type) {
case CASES.NEXT_GREATER:
condition = () => stack.length && arr[stack[stack.length - 1]] < arr[i];
assignmentPos = 'inside';
break;
case CASES.PREV_GREATER:
condition = () => stack.length && arr[stack[stack.length - 1]] <= arr[i];
assignmentPos = 'outside';
break;
case CASES.NEXT_SMALLER:
condition = () => stack.length && arr[stack[stack.length - 1]] > arr[i];
assignmentPos = 'inside';
break;
case CASES.PREV_SMALLER:
condition = () => stack.length && arr[stack[stack.length - 1]] >= arr[i];
assignmentPos = 'outside';
break;
default:
throw new Error('Invalid type');
}
while (condition()) {
let index = stack.pop();
if (assignmentPos === 'inside') {
result[index] = arr[i];
}
}
if (assignmentPos === 'outside' && stack.length) {
result[i] = arr[stack.at(-1)];
}
stack.push(i);
}
return result;
}
// Example usage:
const arr = [4, 5, 2, 10, 8];
console.log(monotonicStackTemplate(arr, CASES.NEXT_GREATER)); // Output: [5, 10, 10, -1, -1]
console.log(monotonicStackTemplate(arr, CASES.PREV_GREATER)); // Output: [-1, -1, 5, -1, 10]
console.log(monotonicStackTemplate(arr, CASES.NEXT_SMALLER)); // Output: [2, 2, -1, 8, -1]
console.log(monotonicStackTemplate(arr, CASES.PREV_SMALLER)); // Output: [-1, 4, -1, 2, 2]